信息存储
大多数计算机使用8位的块,或者字节(byte),作为最小的可寻址的内存单位,而不是访问内存中单独的位。
机器级程序将内存视为一个非常大的字节数组,称为虚拟内存(virtualmemory)。
内存的每个字节都由一个唯一的数字来标识,称为它的地址(address),所有可能地址的集合就称为虚拟地址空间(virtual address space)。
十六进制
| 二进制 | 十进制 | 十六进制 |
|---|---|---|
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
进制转换
十六进制 <=> 二进制
每四位二进制一组,转换成一个十六进制字符。如果位数不够,则向前补0
一位16进制转换成四位二进制
n进制 <=> 十进制
从个位开始,每个位乘以n的m-1次方并相加
(F6C)16 = (15 * 162) + (6 * 161) + (12 * 160) = (3948)10
(1010)2 = (1 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = (10)10
执行步骤,除以 n 得到余数,余数就是每个位的数字。然后继续用商除以n,知道商为0
| 除以 n | 商 | 余数 | 位次 |
|---|---|---|---|
| (100)/16 | 6 | 4 | 0 |
| (6)/16 | 0 | 6 | 1 |
(100)10 = (64)16
寻址和字节顺序
明确:
- 对象的地址是所使用字节中最小的地址,也就是说地址是递增的
考虑一个w位的整数,其位表示为[xw-1, xw-2, …, x1, x0],其中xw-1是最高有效位,而x0是最低有效位。假设w是8的倍数,这些位就能被分组成字节,每8个有效位为一组有效字节。
某些机器选择在内存中按照从最低有效字节到最高有效字节的顺序存储,最低有效字节在最前面的方式称为(little endian)小端法
在内存中按照从最高有效字节到最低有效字节的顺序存储,最高有效字节在最前面的方式称为(big endian)大端法
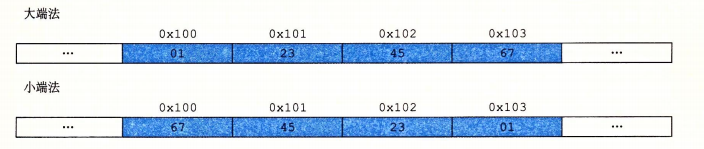
整数表示
机械数和真值
机器数有两个基本特点:
数的符号数值化。通常这个符号放在二进制数的最高位,称符号位,以
0代表符号+,以1代表符号-。二进制的位数受机器设备的限制。机器内部设备一次能表示的二进制位数叫机器的字长,一台机器的字长是固定的。字长8位叫一个字节(Byte),机器字长一般都是字节的整数倍,如字长8位、16位、32位、64位。
真值:
一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是带符号的,在计算机用机器数的最高位存放符号,正数为0,负数为1。
例如二进制真值数 -011011,它的机器数为 1011011。
原码
原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。
(+1)原 = 0000 0001
(-1)原 = 1000 0001
反码
正数的反码是其本身;
负数的反码是在其原码的基础上,符号位不变,其余各个位取反。
(+1) = (0000 0001)原 = (0000 0001)反
(-1) = (1000 0001)原 = (1111 1110)反
补码
正数的补码就是其本身;
负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后+1。(也即在反码的基础上+1)
(+1) = (0000 0001)原 = (0000 0001)反 = (0000 0001)补
(-1) = (1000 0001)原 = (1111 1110)反 = (1111 1111)补
整数运算
根据运算法则减去一个正数等于加上一个负数,即:1-1 = 1 + (-1) = 0, 所以机器可以只有加法而没有减法,这样计算机运算的设计就更简单了。
首先来看原码:
计算十进制的表达式: 1 - 1 = 0
1 - 1 = 1 + (-1) = (0000 0001)原 + (1000 0001)原 = (1000 0010)原 = -2
如果用原码表示,让符号位也参与计算,显然对于减法来说,结果是不正确的。这也就是为何计算机内部不使用原码表示一个数。
为了解决原码做减法的问题, 出现了反码:
计算十进制的表达式:1 - 1 = 0
1 - 1 = 1 + (-1) = (0000 0001)原 + (1000 0001)原 = (0000 0001)反 + (1111 1110)反 = (1111 1111)反 = (1000 0000)原 = -0
这样就会导致(0000 0000)原 和(1000 0000)原 两个编码表示0。
于是补码的出现,解决了0的符号问题以及0的两个编码问题:
1-1 = 1 + (-1) = (0000 0001)原 + (1000 0001)原 = (0000 0001)补 + (1111 1111)补 = (1 0000 0000)补 =(0000 0000)补 =(0000 0000)原
这样0用(0000 0000)表示,而以前出现问题的-0则不存在了。而且可以用(1000 0000)表示-128:-128的由来如下:
(-1) + (-127) = (1000 0001)原 + (1111 1111)原 = (1111 1111)补 + (1000 0001)补 = (1000 0000)补
-1-127的结果应该是-128,在用补码运算的结果中,(1000 0000)补 就是-128,但是注意因为实际上是使用以前的-0的补码来表示-128,所以-128并没有原码和反码表示。(对-128的补码表示(1000 0000)补 ,算出来的原码是(0000 0000)原 ,这是不正确的
使用补码,不仅仅修复了0的符号以及存在两个编码的问题,而且还能够多表示一个最低数。这就是为什么8位二进制,使用原码或反码表示的范围为[-127, +127],而使用补码表示的范围为[-128, 127]。
因为机器使用补码,所以对于编程中常用到的有符号的32位int类型,可以表示范围是: [-232-1, 232-1-1] 因为第一位表示的是符号位,而使用补码表示时又可以多保存一个最小值。
浮点数
二进制小数
(10.111)2 = 1*21 + 0*20 + 1*2-1 + 1*2-2 + 1*2-3
(10.34)10转二进制:
- 整数部分:除以二,余数为二进制位,商继续除以二,直到商为0
- 小数部分,乘以二,整数部分为二进制位,小数部分继续乘以二,直到值为0
IEEE浮点表示
IEEE 浮点标准用 V=(-1)s * M * 2E 的形式来表示一个数:
- 符号(sign) s决定这数是负数(s=1)还是正数(s=0),而对于数值0的符号位解释 作为特殊情况处理。
- 尾数(significand) M是一个二进制小数,它的范围是[1, 2),或者是[0, 1)。
- 阶码(exponent) E的作用是对浮点数加权,这个权重是2的E次幂(可能是负数)
将浮点数的位表示划分为三个字段,分别对这些值进行编码:
- 一个单独的符号位s直接编码符号s。
- k位的阶码字段exp编码阶码E。
- n位小数字段frac编码尾数M,但是编码出来的值也依赖于阶码字段的值是否等于0。
